世の中の中学生は「小数派」かそうでないかの2つに分かれます。
まあ、これを読んだほぼ全ての方は「多数派」じゃねーの?と思うでしょうが、残念です。まだ頭が数学脳になっていませんね。ええ、なりたくありませんね、そんなもの。
中学生は「小数派」と「分数派」の2つに分かれるのです。
ん?どっちも嫌いですと?アーアー聞こえませーん。
目次
小学生気分を引きずる「小数派」
小数派とは、何でも小数で計算しようとする一味のことです。この一派は、割り算の際なんでもかんでも小数で答えを出そうとする傾向があります。
例えば3÷2を計算するとき、答えを1.5とするのが特徴です。
でもこの人たち、2÷3のような割り切れない計算をするときに困ります。すると、「先生、割り切れないときはどうするんですか?」という質問を投げかけてきます。きっと四捨五入する気満々です。
割り算を見たらまず筆算!という思考が小学生時代からプログラムされているので、何も考えずに筆算を始めてしまうのです。果たしてこれは割り切れるのか?なんて予想をせず、まず筆算を始めてしまうのが良くないところです。
もう文章の流れ的におわかりだと思いますが、私はアンチ小数派です。ぶっちゃけ小数が大嫌いだと言っても過言ではありません。
世間に誤解されている「分数派」
多くの小学生に「分数と小数どっちが嫌い?」というと、「分数!」と答えが圧倒的になります。それだけ小学生からは分数受けが悪い。
これは、算数の内容が極端に難しくなる小5後半~小6の印象が非常に悪く、同時期に勉強した分数に対しても同様に難しさを感じるからだと思われます。
その印象を中学に入っても引きずっているため、多くの中学生は分数に対してネガティブな印象を持っています。
わずかなデメリットを除けば、分数計算は圧倒的に小数より簡単です。そのことを気づいていない子がたくさんいるので、この記事を読んだ保護者の方はぜひお子さんに読ませて欲しいと思います。
以下、分数派としてセールストークを繰り広げていきましょう。
小数・分数のメリット・デメリット
小数は計算が遅い
例えば、1.2×0.25の計算をしてみましょう。まず普通の小中学生なら何も考えずに筆算を始めるでしょう。
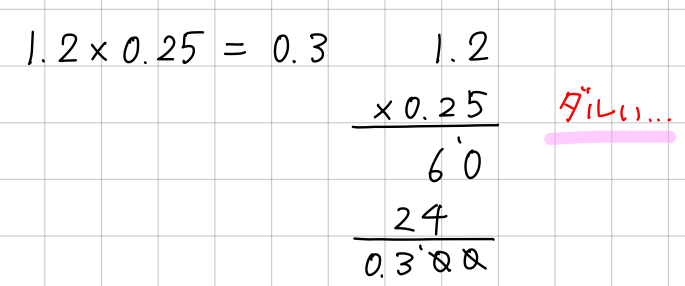
みんな大好き筆算(私は大嫌い)
ちゃんと答えは出ますが、筆算をする手間がある分ミスをする可能性は高いと言えます。
では、今度は6/5×1/4の計算をしてみます。見比べれば分かりますが、先ほどの計算を分数に直しただけです。
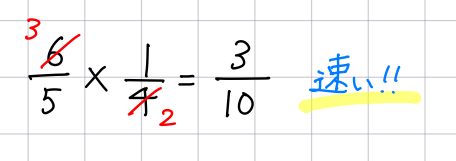
暗算だけで完了!
約分をするだけですから、暗算のみで終わります。極端に苦手な子以外はほぼ正解できるはずです。
別の計算もしてみます。実は今回の記事を書く発端となったのがこの計算です。指導後の質問でとある中3生から聞かれたもので、模範解答が分数で、自分は小数で書いたのはOKなのか、というもの。当然どちらでもOKです。
しかしこの生徒は「小数派」です。そこで簡単な例を挙げて「分数派」のプロモーションをしたというわけ。
実際の説明に使った数字は忘れましたので、適当に3.5の2乗を計算します。これは私も筆算に頼りたくなるところです(実際には電卓を使います)。
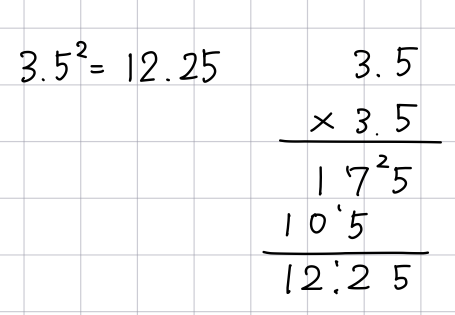
さすがに3.5の2乗は覚えられない
うん、面倒ですね。
さて、3.5は分数に直すと7/2です。これを2乗してみましょう。
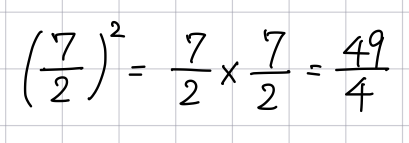
もはや比較にならないお手軽さ
累乗する場合約分はありませんから、本当にただ分母分子をかけるだけ。チョロい。
これを見せられては、その生徒は納得せざるをえません。幸い理解が大変早い子なので、すぐに飲み込んでくれました。
このように、少なくともかけ算や割り算のときは分数派の圧倒的勝利と言っても良いでしょう。
反対に、足し算や引き算のときは通分の手間があるだけ分数は面倒ですが、中学生は分数の足し算・引き算を使うケースが極端に少ないので、余り問題になりません。
計算が不正確
これは、割り算の答えを小数であらわそうとすると、どうしても割り切れない場合があるということ。分かりやすいのが2÷3=0.6666…でしょう。小数で表すことは出来ません。
分数なら、2/3で終わりです。これはピッタリ正確な値を示しているので、速く、かつ正確です。
計算ミスをしやすい
そして、計算の手順が多くなることでミスが多くなること。特に小数の割り算を正確に計算するのはなかなか大変です。小数点をずらしたり、割り切れない場合はどのケタまで計算するか判断したり、四捨五入したり、あまりを出したりと、注意すべきポイントのオンパレードですからね。
事実、小数の計算だらけの小5生の計算ミスの頻度といったら目をおおわんばかりです。
小数と比べれば、分数はせいぜい通分や約分くらいなので、正解率は圧倒的に高くなります。計算ミスはほとんどなく、ときどき約分忘れや約分が途中になってしまうミスがあるくらいでしょう。
およその大きさ感は小数の勝ち
分数最大の弱点は、仮分数のわかりにくさです。
14/5と書いてあると、普通の計算力だと「だいたいいくつくらいなんだろう?」と悩みますよね。帯分数ならそれが解決しますが、今度は変形する手間がかかってしまいます。
一方小数なら2.8です。だいたいいくつくらいか、一目瞭然です。こういった直感的なわかりやすさが小中学生にウケるのかもしれません。
科目による使い分け
これだけ分数をオススメしていますが、科目によって分数と小数の使い分けが決まっているのはご存じでしょうか?
先生は知っていますが、それをハッキリと明言する方はあまりいらっしゃらないようです。
数学は分数で
正確に言うと、数学は分数だろうが小数だろうがどちらでもOKと考えて良いです。つまり、3/2と答えようが1.5と答えようがどっちでも変わりません。もちろん1/3を0.33と答えてはいけません。
どちらでも良いならば、割り切れない事がなく、計算もラクな分数を選ぶのは必然でしょう。
せっかく2x=3からx=3/2と求めたのに、さらに3÷2をやってまで小数に直す必要はどこにありますか?その余計な計算で間違えてしまうより、さっさと分数で答えるようにしたいところです。
理科は原則小数で
ちょっと小難しい話をしますが、理科は厳密に言うと正確な値がほとんどありません。実験で得られる数字は、みな実験装置で計ったものだからです。
例えば、物質1.5gというのは本当に1.5gぴっっっっっっったりなのでしょうか?質量を計ったとき、目盛りの1/10レベルでピッタリに「見える」とき、ようやく1.5g「っぽい」と言えます。でも、目盛りを顕微鏡で見たらもしかしたら1.501gかもしれません。
もっと凄い装置を使って計ったら1.50gかもしれません。これは、小数第2位までは正確だよ!と宣言しています。
分数で3/2gと書いてしまうと、どこまで正確に計った測定値なのか区別できません。理科においては1.5と1.50は意味が違うのです。
そのため、基本的に小数を使います。
計算は分数でやろう
計算は分数の方が優れているわけですから、うまく使い分けが必要です。
理科でも数学でも、計算は基本的に分数で進めていくと良いです。数学の場合はそのままフィニッシュで構いません。
理科は最後に小数へ直す必要がありますので、これ以上計算出来ないところまで分数で計算をしていき、最後に小数に直してあげれば手間が最も少なくて済みます。
実際に、3.0Vの電圧をかけて0.12A流れたときの抵抗値を計算してみます。
小数だと筆算が必要なレベルでしょう。中学生は小数点を2つずらして計算するところで意外にミスします。怖い怖い。
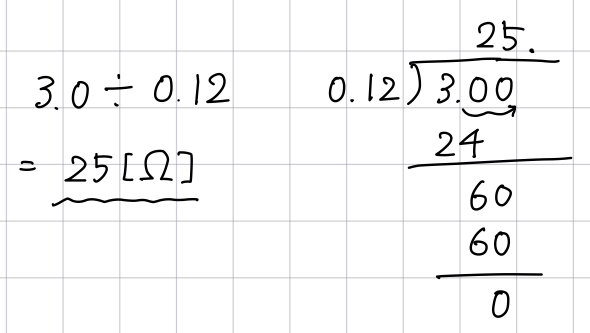
とはいえ大した計算ではありませんが
それが分数の場合、約分をちまちましていくだけです。ある程度約分をしたら、最後に割り算をします。

100÷4のラッキー感は異常
ここでポイントなのが、約分によって数字が小さく、簡単になっているんですよね。多少計算を鍛えている子なら、暗算で片がつくことも少なくありません。
同じ小数で答えるにしても、途中で分数計算をしていくことで、だいぶ計算の負担を軽くすることが出来るのです。
まとめ
私は中学生の授業の早い内に「分数派」のメリットをことあるごとに伝えます。中1の最初から通っている生徒なら、かなりスムーズに洗脳、もとい浸透していきます。
問題は自己流でずっときた子。もちろん「小数派」でもキチンと答えは出るのですが、もっと速く楽に解ける方法を意識することなくきてしまいます。一度身についてしまった習慣はなかなか抜けにくいので、かなりしぶとく言わないとなかなか改善しません。
最終的にはテストのとき時間が足らなくなって、解けるはずの問題を落としてしまう結果になりかねません。小数・分数の話に限らず、塾で言われた計算のアドバイスは素直に身につけた方が良いですよ。
ただ、生徒がどのような計算過程をしているかは、なかなかチェックできません。生徒が演習しているときに机間巡視をくまなく行うのも良いですし、私のようにノートチェックを通じて確認するのもアリです。
「結果的にできればいいじゃん」と言っているうちはなかなか伸びません。せっかく塾に通うのですから、ぜひ効率の良い方法を身につけて一歩リードしていきたいところですね。
計算に関する細かな持ちネタはたくさんあります。私が計算嫌いっ子だったので、ラクな方法探しは必死にやりましたからね(笑)
おいおいオープンにしていくつもりです。チェックしてみてください。
この記事を書いた人
- 螢田教室・板橋教室責任者
- 指導歴20年の理系担当講師。
Twitter始めました。ブログは長文、それ以外はTwitterで情報を発信していきますので、よろしくお願いします。
最近の記事
 勉強法2024年6月15日ワークは何も見ないで解こう!調べながら解いてはいけない理由
勉強法2024年6月15日ワークは何も見ないで解こう!調べながら解いてはいけない理由 小学生2023年7月7日小学生が絶対にマスターすべき算数まとめ
小学生2023年7月7日小学生が絶対にマスターすべき算数まとめ 高校進学2022年2月15日令和4年度 神奈川県公立高校学力検査 理科の難易度分析
高校進学2022年2月15日令和4年度 神奈川県公立高校学力検査 理科の難易度分析 高校進学2022年2月1日【令和4年度】2022年度神奈川県公立高校志願変更前倍率の考察
高校進学2022年2月1日【令和4年度】2022年度神奈川県公立高校志願変更前倍率の考察















